Dimensions

Réussirais-je à vous faire toucher du doigt l’intouchable ?

Rien de cochon dans ce titre, calmez-vous ! Je parle de vulgarisation (du latin vulgus = le peuple, ce qui est compréhensible par tous).

À travers un certain nombre d’exemples judicieusement choisis (faites-moi confiance), je vais tenter de vous faire percevoir (si ce n’est comprendre) les concepts qui sous-tendent certaines réalités de la physique moderne. On verra d’ailleurs les limites de l’exercice pour deux raisons essentielles :

Tout d’abord, on ne peut comprendre parfaitement une civilisation que lorsqu’on en maîtrise les subtilités de la langue. Il en est de même en physique. Il arrive un moment où la méconnaissance des mathématiques de haut niveau nous bloque dans une compréhension plus poussée (ce n’est pas pour rien que je m’inclus dans cette catégorie).

De plus, certains concepts demandent une faculté d’abstraction ou d’imagination qui, si elle est plutôt bien répandue chez les amateurs d’imaginaire que nous sommes, reste malgré tout partagée à des degrés divers. Je précise qu’il n’y a aucune notion de « supériorité » ou « d’infériorité » dans ces derniers propos. Je ne me sens pas dévalorisé parce que je suis incapable de réaliser un dessin de Manchu ou de Caza (mais je les admire beaucoup, cela va sans dire).

Donc, accrochez-vous, c’est parti !

1-Analogie

Voilà quelque chose de bien pratique. Il s’agit de prendre des comparaisons dans un domaine que tout le monde comprend en espérant ouvrir l’esprit au niveau supérieur.

Exemple : nous sommes tous capables (quand on possède une vision ordinaire) de percevoir que notre environnement est à trois dimensions. Mais comment concevoir un monde qui posséderait quatre dimensions d’espace ?

Pour y arriver, je vais vous aplatir (cette analogie est utilisée dans le roman Flatland de E.Abott). Considérez que vous ne possédez que deux dimensions. Vous êtes des êtres plats qui vivez à la surface d’un plan. Quand vous rencontrez un carré, vous ne voyez que l’un des côtés du carré, sous forme d’une ligne. Deux, si vous vous placez à un angle. En admettant qu’il y ait une ouverture sur l’un des côtés, vous êtes contraints de passer par cette ouverture pour pénétrer à l’intérieur du carré.

À présent, vous êtes un extraterrestre (par rapport à ce monde plat) : vous possédez trois dimensions. Vous « survolez » ce monde plat et vous avez le pouvoir d’en percevoir la totalité d’un seul regard. Jugez plutôt : vous embrassez d’un seul coup d’œil les quatre côtés du carré en même temps que son intérieur et son extérieur. En utilisant cette troisième dimension, vous avez même la possibilité de passer de l’intérieur à l’extérieur du carré sans franchir l’ouverture. Étonnant non ?

Nous sommes à présent capables non pas de nous représenter, mais de concevoir ce que pourrait percevoir un être se déplaçant dans quatre dimensions d’espace. Il pourrait voir sans bouger l’ensemble des murs, planchers, plafonds de nos maisons, et pourrait y pénétrer sans passer par les portes. Si vous avez besoin d’une interprétation scientifique des fantômes, servez-vous !

Toujours en se référant à ce qui se passe en deux dimensions, on peut s’approcher de la représentation d’un objet à quatre dimensions. Comment représente-t-on un cube sur une feuille de papier ? On peut, par exemple, tracer un premier carré, puis un deuxième légèrement décalé et relier les sommets deux à deux. On obtient une projection à deux dimensions de notre cube.

De la même façon, prenez un cube puis un deuxième cube légèrement décalé, reliez les sommets deux à deux, et vous obtenez la projection tridimensionnelle d’un hypercube. Voici une illustration tirée de La quatrième dimension de Thomas Banchoff pour plus de clarté.

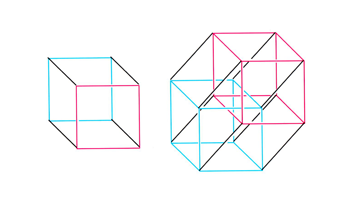
Bon, me direz-vous, c’est un petit jeu amusant, mais à quoi ça sert ?

Passons donc aux choses sérieuses.

2-Courbures spatiotemporelles

Les masses courbent le continuum spatiotemporel. Ça calme hein ? Ce n’est pas moi qui le dis c’est Einstein, donc je m’incline. Quelles sont les conséquences de cette courbure ?

Tout d’abord, la gravitation ne doit plus être perçue comme une force qui attire les corps, mais comme le résultat du parcours des corps dans cet espace courbe. La lumière elle-même ne se propage pas en ligne droite à proximité des grosses masses. Nous parlons ici de masses aussi importantes qu’une planète ou une étoile (l’effet existe pour les petites masses, mais il est infime)

Pour arriver à nous représenter ce qui se passe, nous allons nous servir de notre modèle à deux dimensions. Ce continuum à deux dimensions se comporte comme une feuille de caoutchouc. Quand on pose une boule dessus, cette feuille se déforme.

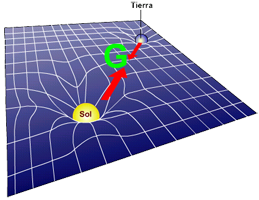
(source : Wikipedia)

Le point le plus court d’un endroit à un autre n’est plus une ligne droite, mais une courbe appelée géodésique.

Les corps suivent ces géodésiques qui ont tendance à les rapprocher de l’objet qui est cause de cette déformation : voilà pour la gravitation. La lumière suis également ces courbes (et ne parcoure pas la même distance que si la ligne était droite). Il faut donc en tenir compte dans certains calculs pointus. Si l’on ne tenait pas compte de cet effet dans les calculs de triangulation liés aux GPS, on ferait des erreurs de plusieurs centaines de mètres.

Vous m’avez suivi ? Vous n’aurez donc aucune difficulté à revenir à nos trois dimensions d’espace, et à concevoir que cette courbure se produit de la même manière. Quand vous lâchez un objet, il tombe par terre, car il suit une géodésique qui le rapproche du sol. La lumière suit des trajectoires courbes qui nous montrent des effets variés. Par exemple :

Pendant une éclipse de Soleil, les étoiles et les planètes que l’on aperçoit à proximité immédiate de l’astre du jour ne sont pas exactement à la place où on les voit. Ou encore, les grands amas de galaxies jouent le rôle de loupe et nous permettent d’apercevoir des galaxies beaucoup plus lointaines, mais très déformées (on appelle ça « arcs gravitationnels » que vous pouvez distinguer sur la photo suivante).

(Source : Ciel & Espace)

3-Topologie de l’univers

Je vous préviens tout de suite, si vous n’avez pas encore de nœuds au cerveau, ça ne saurait tarder.

Dans le chapitre précédent, je vous parlais plutôt de géométrie. Nous abordons avec la topologie ce qui concerne la forme et les propriétés du « lieu univers ». Il va vous falloir ici une bonne dose d’imagination, car même l’analogie à deux dimensions n’est pas facile à saisir.

Je vais me contenter d’aborder deux exemples. Sachez simplement que plusieurs théories sont étudiées, et que, même si les dernières observations tendent à confirmer l’un des groupes de théories, tout est loin d’être résolu.

Notre univers à deux dimensions (vous commencez à être familiarisé avec cette analogie) est courbe. Je ne parle plus ici des courbures locales engendrées par tel ou tel corps, mais bien d’une forme générale. On obtiendrait par exemple la surface d’une sphère.

Vous la voyez ? Rien de compliqué ? Une belle sphère à trois dimensions… Stop ! J’ai bien parlé de la surface à deux dimensions d’une sphère. Dans ce modèle à deux dimensions, seule la surface de la sphère représente l’univers, le reste n’a pas d’existence. Cela signifie en clair que mon univers à deux dimensions n’est pas courbé dans une troisième, puisque la totalité de l’univers est contenue dans cette surface et qu’il ne peut rien y avoir « en dehors » sans contredire la notion de « totalité » que je viens d’évoquer.

En d’autres termes, vous (oui vous !), être à deux dimensions rampant à la surface de ce que vous percevez comme un plan (puisque par définition vous êtes incapable de concevoir une troisième dimension), serez fort surpris de vous retrouver à votre point de départ si vous avancez suffisamment longtemps dans la même direction.

Avez-vous réussi à concevoir l’existence de cette surface courbe comme unique chose existante ? Mathématiquement ce n’est pas un problème en tout cas.

Pour notre univers (on gardera trois dimensions d’espace et une de temps pour ne pas compliquer), ce pourrait être pareil. Ce volume, ce continuum spatiotemporel, pourrait être courbe de telle sorte qu’un voyageur spatial (et quasi-immortel) pourrait revenir à son point de départ en se dirigeant dans la même direction. Ne me demandez pas dans quoi notre univers est courbé. À l’instar de la surface de la sphère, il est courbé point ! Puisque l’on considère que l’univers est tout, la notion de « dehors » n’a pas de sens.

Une petite dernière pour la route ?

Vous connaissez sans doute ces jeux vidéo dans lesquels sortir par un côté de l’écran vous fait rentrer par l’autre. Tout se passe comme si le côté gauche touchait le côté droit et que le haut touchait le bas. Votre écran est, dans ce cas, la représentation plane d’un tore.

Fabriquer un tore à partir d’un carré de papier est facile. Faites d’abord un tube en rapprochant le côté haut du côté bas. Puis courbez le tube pour rapprocher la gauche et la droite (il n’y a sans doute qu’en physique que c’est possible…). Voilà votre tore. On comprend alors comment dans ce type d’espace courbe, gauche et droite se rejoignent ainsi que haut et bas. Encore une fois, comme dans l’exemple de la sphère, nous ne considérons ici que la surface du tore. L’image ci-dessous tirée de L’univers chiffonné de Jean-Pierre Luminet vous montre la fabrication du tore.

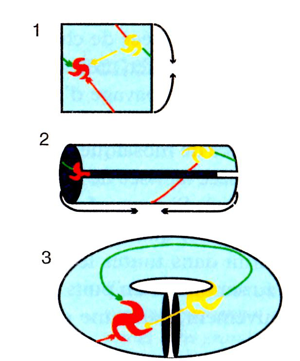
Pour un univers hypertorique (revoilà nos trois dimensions) il faudrait partir d’un cube et courber ce cube de façon à rapprocher les faces droite et gauche (on voit à peu près : ça ressemblerait à un tore de section carrée) en même temps que les faces haute et basse (oui, oui, avec un peu d’imagination) ainsi que les faces avant et arrière (heu…)

Certains modèles partent même d’un dodécaèdre dont les douze faces se répondent deux à deux avec une légère rotation (Jean-Pierre Luminet).

Vous voyez ?

Moi non plus ! Je vous souhaite le bonsoir.